It's not always easy to find the formula you need, and impossible to remember them all, so here's a collection of some I have found useful.
| sin A, cos A |
| sin2A + cos2A = 1 |
| sin2A = (1 - cos 2A)/2 |
| sin A = 1 / cosec A & sin A = cos A tan A |
| sin (A+B) = sin A cos B + cos A sin B sin (A-B) = sin A cos B - cos A sin B |
| sin 2A = 2 sin A cos A |
| sin A - sin B = 2 cos (A+B)/2 sin (A-B)/2 sin A + sin B = 2 sin (A+B)/2 cos (A-B)/2 |
| sin2A - sin2B = sin (A+B) sin (A-B) |
| Write tan θ/2 = t ... then sin θ = 2t / (1 + t2) ... and cos θ = (1 - t2) / (1 + t2) |
| sinh x, cosh x, tanh x |
| π radians = 180 degrees |
| 1 radian = 57.3 degrees |
| sinh x = (e x - e -x ) / 2 |
| cosh x = (e x + e -x ) / 2 |
| tanh x = sinh x / cosh x |
| cosh2x - sinh2x = 1 |
| ex = sinh x + cosh x |
| log, ln |
| log10 e = 0.43429 |
| loge 10 = ln 10 = 2.30259 |
| n log x = log xn |
| Roots of a quadratic |
| If y = a x2 + b x + c then ... |
| x = [ -b ± √( b2 - 4 a c)] / 2a (2 roots) |
| Stray capacitance |
| Capacitance between 2 plates in air is ... |
| 0.9 pF /sq.cm. /mm separation |
| Approximations |
| Provided that d <<1 ... |
| 1 / (1 - d) ≈ 1 + d 1 / (1 + d) ≈ 1 - d |
| (1 ± d)n ≈ 1 ± nd |
| sin A, cos A |
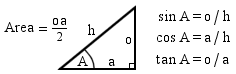 |
| cos A = 1 / sec A & cos A = sin A / tan A |
| cos2A = (1 + cos 2A)/2 |
| cos (A+B) = cos A cos B - sin A sin B cos(A-B) = cos A cos B + sin A sin B |
| cos 2A = cos2A - sin2A |
| cos B - cos A = 2 sin (A+B)/2 sin (A-B)/2 |
| 1 - sin A = coversin A |
| cos2A - sin2B = cos (A+B) cos (A-B) |
| Complex numbers where j = √-1 |
| (a + jb) = √ [a2 + b2] tan-1(b/a) |
| e j θ = cos θ + j sin θ e -j θ = cos θ - j sin θ |
| cos θ = (e j θ + e-j θ ) / 2 sin θ = (e j θ - e-j θ ) / 2j |
| e jnθ = cos nθ + j sin nθ |
| n (cos θ + j sin θ) = cos nθ + j sin nθ |
| Geometric progression |
| If a series is a, ar, ar2, ar3, then ... |
| nth term = a r(n-1) |
| Sum of first n terms is S = a (rn - 1) / (r - 1) |
| Energy in a capacitor |
| If a capacitor C is charged to V, then |
| Energy stored (joules): J = C V2 / 2 |
| Energy in an inductor |
| If an inductor L is carrying I amps, then |
| Energy stored (joules): J = L I2 / 2 |
| Small angles |
| Provided that d (radians) is very small ... |
| sin d ≈ d & sinh d ≈ d |
| cos d ≈ 1 & cosh d ≈ 1 |
| tan d ≈ d & tanh d ≈ d |
| tan A |
| tan A = sin A / cos A .. & .. cot A = 1 / tan A |
| 1 + tan2A = sec2A .. & .. 1 + cot2A = cosec2A |
| tan2A = (1 - cos 2A) / (1 + cos 2A) |
| tan (A+B) = [tan A + tan B] / [1 - tan A tan B] tan (A-B) = [tan A - tan B] / [1 + tan A tan B] |
| tan 2A = 2 tan A / (1 - tan2A) tan (A/2) = sin A / (1 + cos A) |
| tan A + tan B = sin (A-B) / cos A cos B tan A - tan B = sin (A+B) / cos A cos B |
| cot A + cot B = sin (A+B) / sin A sin B cot A - cot B = sin (-A+B) / sin A sin B |
| Binomial theorem |
| (1 ± x)n = 1 ± nx ± n (n-1) x2/ (1 . 2) ... ... ± n (n-1) (n-2) x3/ (1 . 2 . 3) ... etc |
| e |
| e = 1 + 1 + 1/(1 . 2) + 1/(1 . 2 . 3) ... ... + 1/(1 . 2 . 3 . 4) ... etc ... = 2.71828 |
| ex = 1 + x + x2/(1 . 2) ... ... + x3/(1 . 2 . 3) + x4/(1 . 2 . 3 . 4) ... etc |
| Arithmetic progression |
| If a series is a, (a+d), (a+2d), (a+3d), then ... |
| nth term = a + (n - 1) d |
| Sum of first n terms is S = a n + (n - 1) n d / 2 |
| Root-mean-square (RMS) |
| If a sinewave voltage has a peak value of ± E, then |
| Erms = E / √2 |
| Mnemonic for π |
| How I Need A Drink, Alcoholic Of Course ... |
| ( π = 3.1415926 ... ) |
| Conversions |
| One pound (lb) = 454 grams |
| One mile = 1,760 yards = 5,280 ≈ 5,000 feet |
| One year = 8,760 ≈ 104 hours |
| A gallon of water weighs 10 lb. (in UK!) |
| One horse-power = 746 watts |
| One atmosphere = 14.7 psi = 1013 mb |
| One mile per hour = 1.467 ≈ 1.5 feet/sec |
