What's charge?
Charge (Q) is a sort of local distortion in space that makes nearby objects behave in unexpected ways.
For example, if you can get charge onto a balloon, it will stick to a wall instead of floating down to the ground. A charged glass or plastic rod will attract small pieces of paper.
How do you get charge onto the balloon?
The easiest way is to rub it vigorously on a woollen jumper. It is believed that all materials have some charge on their surface, and rubbing the surfaces together encourages the charge to collect where you want it. Some materials transfer charge better than others. Fur works well, and so does silk.
How long has this been known?
The ancient Greeks knew about it 2500 years ago. Their favourite materials seem to have been amber and cat's fur, but how bored would you have to be to enjoy polishing a piece of amber on a cat? They made their own entertainment in those days.
Why is it called electric charge?
The Greek word for amber - fossilised tree sap (left) - is apparently elektron, so the phenomenon became known as "electricity". It had a name, but nobody understood what it was or how it worked (or indeed what use it might be.)
Is there more than one type of charge?
Experiment showed that there are two types. A French physicist found (in 1733) that if he rubbed sealing wax with cat's fur instead of rubbing a glass rod with silk, he got different results. Some objects were attracted to the rod, but were repelled by the electrified wax. And objects attracted to the wax were repelled by the rod. Evidently, there were two types of electricity, which he named 'resinous' and 'vitreous'.
Twenty years later, Benjamin Franklin decided it was more sensible to call the two types of electricity 'positive' and 'negative'. After many experiments, it was eventually realised that moving a lump of positive electricity to one place meant that an equal sized lump of negative electricity was left behind. All that rubbing simply separated the positive and negative charges.
Is positive charge simply the opposite of negative charge?
Yes. Put them together and they seem to cancel each other out and disappear.
How much force can charge exert?
That depends on how much charge you can pile together in one place. Modest amounts don't do much, but if you can accumulate a lot you can make your own lightning. The lightning in thunderstorms is probably caused by positive and negative charges being somehow forcibly separated inside clouds, and a lightning strike is a brief current of more than 10,000 amps.
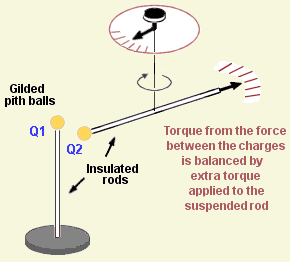
What controls the size of the force?
The force between charges is greater when they are close together. The physicist Coulomb built a special rig to test this. One charge was fixed in place, and the other was free to move on the lowest-friction bearing he could think of - it was attached to a rod suspended on a silk thread. The charges themselves were induced onto a conductor (thin gold sheet) wrapped around an insulator (dried pith).
He found that the force is proportional to the size of the charges, and decreases with the square of the distance between them. This was enormously helpful, because it led to a clear and simple way of describing (though not explaining) what was going on.
What's Coulomb's law?
It's more useful to write Coulomb's law as a formula (left) that links the measurable quantities in a clear and unambiguous manner, but if you are allergic to algebra, it's not essential. The point is that the force is proportional to the size of the charges (Q1 and Q2), and inversely proportional to the square of the distance (r) between them.
If these quantities are proportional, we can include a constant K and write a proper equation.
Quantities in equations have units. That's what makes them useful. Force is measured in Newtons (N) and distance in metres (m), but what kind of units should be used for Q1 and Q2?
When I first studied physics back in the 1950s, force was measured in 'dynes' (1 dyne = 10μN), and distance in centimetres. Choosing these units made the constant vanish (that is, it made K=1), as long as charge was expressed in something called 'electrostatic units'. This confused me. What was an electrostatic unit?
The answer I got was: it's the quantity of charge that causes a force of 1 dyne between charges 1 cm apart, as the equation states. In other words, don't worry about what charge is, concentrate on what it does!
It took me a long time to realise that an electrostatic unit is nothing more than a current that happens not to be moving.
Does the force Coulomb measured depend on whether charge is positive or negative?
The size of the force doesn't change, but its direction does. Charges of the same type repel each other. The charge on a ball spreads out all over the surface, as each tiny scrap of charge tries to move as far away as possible from its neighbours. But if one ball is positively charged and the other negatively charged, the balls move towards each other. Opposite charges attract each other.
Is charge something to do with atoms?
Definitely. Faraday experimented with electrolysis (in 1833) - passing an electric current from a battery through tanks of water in which various materials had been dissolved. He found that, for example, the quantity of electricity needed to liberate 1 gram of hydrogen (H: atomic weight 1.0) from a tank of water was the same as that needed to extract 107.1 grams of silver (Ag: atomic weight 107.9) from a tank containing a silver compound in solution. The electricity seemed to be breaking chemical bonds within molecules.
Can charge float about in the air, like dust?
Not quite. Charge can attach itself to dust, and especially to tiny fragments of broken molecule. After 1895 it was found that air irradiated with the newly discovered X-rays became conductive. This was thought to be because some atoms or molecules of air had been broken in two, one piece carrying negative charge and the other, positive. The charged fragments were called ions.
What's an electric current?
A current is a stream of moving charge. The amount of charge (that is, the quantity of electricity) is measured in coulombs. A current of 1 amp means 1 coulomb moving for 1 second. A coulomb is 3,000,000,000 electrostatic units!
What's electricity?
Nobody knew quite what it was. As late as 1897, even Lord Kelvin thought that electricity might well be a 'continuous homogeneous liquid', because it flows through conductors like water flows through pipes. Or maybe it was 'atomic', as Faraday had believed. There were two schools of thought, and Kelvin wasn't sure. It was Millikan who settled the argument.
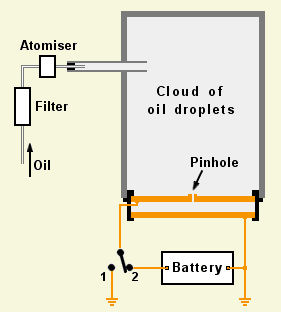
Why did Millikan look at oil drops?
Robert Millikan was an American physicist who in 1910 decided to see if he could find out what charge is by weighing tiny charged objects.
He built a chamber and squirted tiny charged drops of oil into it. As the drops drifted downwards, one or two of them fell through a pinhole into the space below. Millikan set up a short-focus telescope and peered through a window at the drops as they floated slowly down through the lower chamber.
He had arranged things so that the top and bottom walls of this chamber were metal plates connected to a high-voltage battery. When he applied a voltage between the plates, the oildrops' behaviour changed. With the battery connected one way round, the drops fell faster. When it was the other way round, they rose instead of falling, and if he got the voltage just right, he could almost make them hover.
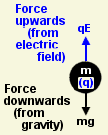
The battery was creating an electrical stress (known as a field) between the plates, even though no current was flowing. This stress applied a force to the charged drops, accelerating them upwards or downwards depending on which way round he connected the battery.
Millikan chose to watch a positively-charged drop that was accelerated upwards, and observed it for several minutes. It rose steadily whilst the battery was connected (as far as the top dotted line in the diagram below). When it reached there he disconnected the battery and short-circuited the plates. Now it fell steadily (down to the bottom dotted line) until he re-connected the battery again. But he noticed something rather odd happening. The drop always fell at the same speed, but sometimes it rose more slowly than it had originally. The graph below is derived from his original measurements, which were taken with a stopwatch.
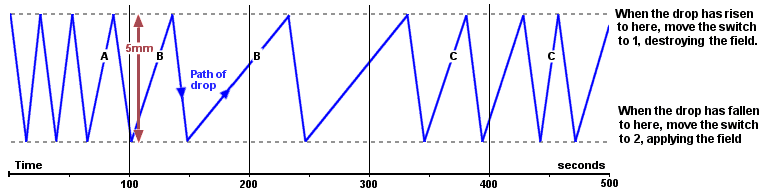
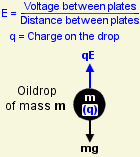
If the oildrop was rising more slowly, the field was not pulling it up as strongly. The upwards force (qE) was smaller. But the voltage hadn't changed, so it must have been the charge (q) that had got smaller. Yet since the drop always fell at the same speed, the weight of this extra charge was negligibly small.
He realised that this positively-charged drop was rising more slowly [as at A] because it had lost some charge. When it rose more slowly still [B], it must have lost even more. But when it rose more quickly again [C], it had somehow gained charge.
The extra charges must have come from ions - tiny charged fragments - smashing into the drop, changing its charge, but not its mass. Negative ions would have cancelled some of its positive charge, effectively reducing its total charge, and positive ions would have put some positive charge back again.
But the really interesting discovery was that the speed of the oildrop always changed by the same discrete amount. He was seeing the effect of individual charges hitting the drop, and they were always the same size! Charge came in fixed amounts, after all. Electricity was not a 'continuous homogeneous liquid' as Kelvin had speculated.
What's more, he was in a position to establish the size of this minimum quantity of charge. This is Nobel Prize level work, quite literally - Robert Millikan was awarded the Physics Prize in 1923.
How can you measure charge with a stopwatch?
The key assumption is that the drop moves at a velocity proportional to the forces acting on it, so writing u as the velocity downwards, and v as the velocity upwards, the ratio of these velocities will be
and then re-arranging to get the charge q that caused this particular v:
After an ion has hit the drop, its charge has changed to q1 and its upward velocity slowed to v1 (assuming that the total charge is reduced after impact, of course) but its downward velocity is still u, so now it's possible to write an equation for e, the tiny amount of charge carried by the ion:
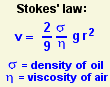
The only quantity in this equation that can't be measured directly is m, the mass of the drop. Fortunately, it can be calculated. Stokes' law predicts how fast a spherical drop of radius r and density σ will fall though a medium of viscosity η. Both σ and η are known, so r can be calculated. Then the mass of the drop can be found from m = (4/3) π r3 σ.
How big is the ionic charge e?
Millikan decided on the basis of very many measurements, and after carefully testing his assumptions, that the correct value was
. . . . . e = 4.774 x 10-10 electrostatic units.
In other words, an 'electrostatic unit' is the total charge carried by about 2 billion electrons.
Why couldn't they just have told me that when I asked?
Prompted by long-ago lectures by Alf Stokes, a wise and gentle man who tried to teach me to think for myself.
Sources
The electron - Robert Andrews Millikan (Univ. of Chicago Press, 1917).