What makes water flow?

How fast will it flow?

Real pipes in real houses

How much pressure is needed?

What size pipe do you need?

How fast will the water flow?

Water Flowing in Pipes - real systems (2)

In this section I show how to calculate the flow-rate in a real domestic water-supply system by using a couple of design tools that link flow-rate to the available head - the pressure that makes the water move. The worked example starts here . If all you need is the graph that links flow rate to the rate-of-pressure-drop for standard pipe sizes, it's here .

But before I design a water supply system for a real house, I should explain how the apparently impossible calculation problems involving turbulent flow can be quickly and easily tackled in practice.

How much pressure is needed?

If the water has to move at a couple of metres per second, or thereabouts, how much pressure is needed?

It's a simple question, but unfortunately there is no simple answer. It depends on what pipes are fitted, and how long they are. Each case must be individually calculated. But don't despair - the calculation is very easy.

The main thing to remember about pressure is this:

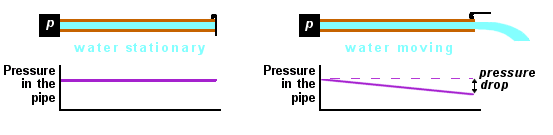
Pressure supplies the energy to push the water along the pipe. Each bit of pipe resists the flow. Energy is lost as the water moves along the pipe, so the pressure falls too. There's a pressure difference between the ends of the pipe.

The longer the pipe, the more energy is lost, and the greater the pressure drop. The rate of pressure drop (that is, the pressure drop per metre of pipe) depends on the pipe diameter and the speed of flow, as you would expect.

The design goal is to choose the pipe sizes that will give the flow rates you want. Each length of pipe wll have a pressure drop along its length. So the aim is to choose pipes that will drop just enough of the available pressure (from the header tank, or from the mains water supply in the street) to give the required flow rates. This means checking the pressure drop along each pipe.

Pressure difference calculation

One way to find the pressure difference between the ends of a pipe is to use the Darcy-Weisbach equation I mentioned in part 1. This predicts how much pressure would be needed to push the water along a pipe at a particular speed. The formula looks like this:

Here, the pressure difference P needed to achieve a flow velocity v depends on the length L and diameter D of the pipe as well as the density of the fluid (ρ - about 1,000 kg/m³ for cold water). It also depends on f, a fiddle factor - sorry, "friction factor", which is included to account for the effects of the Reynolds number. This graph (and its equation) shows the relationship between Re and f.

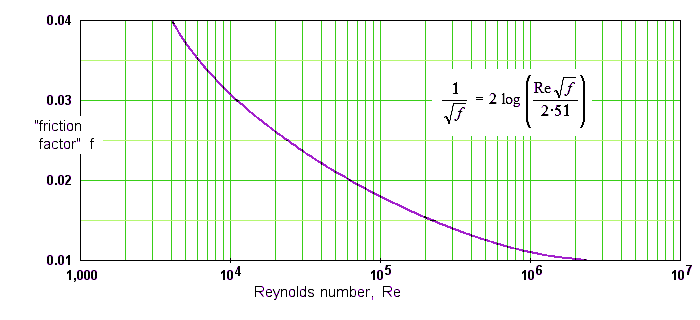
The equation includes √f on both sides, and looks impossible to solve. In fact, it was quite straightforward. The trick is to begin by guessing a value for f (say, 0.01), putting this value (and Re) in the right-hand side, working out the value of the left-hand side, and hence finding f. This new value for f is closer to the actual value than the initial guess, so you plug it back into the right-hand side and do the calculation again . After a couple of iterations the answer is usually close enough to be useful. (By the way, the friction factor used by American engineers is for some reason four times bigger than this. But then, most things in America are bigger than they are in England.)

The graph appears to show that the "friction factor" decreases as the Reynolds number goes up. More speed giving less friction? Hardly likely, is it? In fact, that's not what the graph is saying. The "friction factor" is purely a measure of how the pipe affects the flow, and as the water becomes more turbulent the pipe itself plays a smaller part in events.

If you're more comfortable with pressure expressed as the head in feet, the conversion factor is:

A head of 1 foot of water  ≈  3,000 N/sq.m.

So 28,000 N/sq.m. is about the same as a head of 9 feet (or 3m) of water. But if the head is not exactly 9 feet - and in practice, Sod's Law says it won't be - the water will flow at a different speed! More on this later.

Pressure difference from a graph - the basic design tool

The equations are useful if you ever need to calculate accurately, but in practice it's easier to check from a graph that what you plan to do will work.

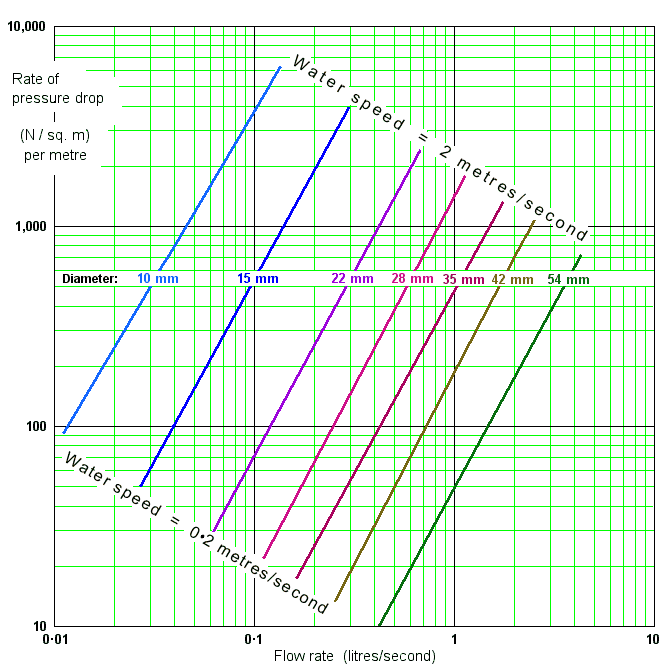
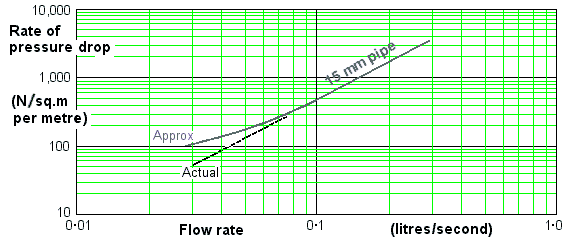
This graph shows pressure drop per metre for a given flow rate and pipe size. You'll find something similar in the relevant British Standard. It was constructed from the pressure-drop equation and covers water speeds from 2.0 m/sec (at the top) down to 0.2 m/sec, and is valid for all normal temperatures. It's saying that the pressure drop along a length of pipe is (nearly) proportional to the square of the flow rate in the pipe.

The graph tells you nearly all you need to know. Use it like this:

What size pipe do you need?

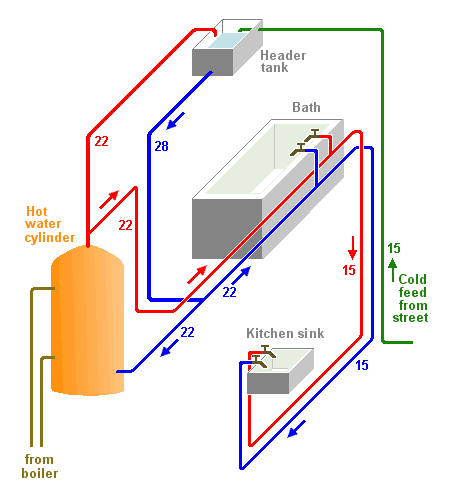
How do you go about choosing the correct sizes for all the different pipes in the house?

Here's a simplified sketch of the hot- and cold-water supply system in a two-storey house. The cold-water header tank in the loft feeds a bath on the first floor, and the kitchen sink on the ground floor. It also feeds the hot water pipes via the cylinder.

The first step is to sketch the layout and choose the pipe sizes such that the water flows fast enough to fill the bath and the sink in a sensible time.

Then calculate what will actually happen, and decide whether anything needs to be changed.

So, here:

• To fill a 10-litre kitchen sink in half a minute, the flow rate of the pipe feeding it must be close to 0.3 litres/second, and 15mm pipe can probably handle this.
• The flow rate for a bath should be higher, but as a single 22mm pipe can comfortably deliver more than 0.5 litres/second, two 22mm pipes (hot and cold) will be more than adequate.

This house doesn't have a shower. Showers use about 10 litres per minute - that is, about 0.17 litres/second - so 15mm pipes would be quite big enough if the owner ever decided to install one. A five-minute shower only uses about 30 litres of hot water. That's why it's cheaper to shower than to have a bath. It's cheaper still when you share with a friend, apparently.

Cold water pipes

The design starts with the cold feeds. The kitchen sink needs 0.3 litres/sec, and according to Table 4 a 15mm pipe will only deliver 0.22 litres/sec at a water speed of 1.5 metres/sec. The choice is, to pay more and use 22mm pipe, or to fit 15mm pipe and put up with a small amount of extra noise. Which would you go for?

A cautious person might ask, how much more noise? A mountain stream, or Niagara Falls?

That's easy to answer. Increasing the flow rate by 30% means that the water flows 30% faster - 2.2 metres/sec instead of 1.5 m/s. The noise level would roughly double. That shouldn't be a big problem.

The kitchen sink cold feed can therefore be 15mm, at least up to the junction with the bath cold feed. The pipe from here to the bottom of the cylinder serves two purposes, though. Someone might be running a bath whilst someone else is downstairs washing up. What then?

Suppose that the bath cold tap and the kitchen sink cold tap are both running at once, with 0.3 litres/sec going to the sink downstairs and (say) 0.5 litres/sec going into the bath. The total flow-rate would be 0.8 litres/sec, and 15mm pipe would complain at that. Will 22mm pipe do, or should it be 28mm? You might ask how likely is it that both taps would be on at the same time, and if it did happen, would anyone mind too much if the cold flow slackened off for a few seconds? Probably not (unless they were having a shower!) 22mm pipe should be adequate.

Finally, there's the pipe from the header tank to the bottom of the cylinder. This one is more important than it looks - it not only carries cold water to the taps but also refills the cylinder as hot water is taken from the top. Water flows through this pipe to every tap in the house. It would be sensible to make it 28mm, which can carry over a litre per second.

Hot water pipes

The hot-water pipes are easy to size, because the thinking has already been done for the cold pipes. The kitchen sink will be fed in 15mm from the tee under the bath, and then in 22mm from the top of the cylinder.

The vent pipe leading from the cylinder to above the header tank should also be 22mm (as local authority planning laws usually require). This pipe is only there as a safety measure - if something goes wrong, and the water in the cylinder boils, it can siphon up safely into the tank instead of bursting the cylinder and ruining all the carpets.

What's the actual flow rate?

It's all very well calculating pipe sizes by assuming a flow rate, but what will actually happen in a real house in practice? How fast will the water flow out of the kitchen sink tap? How long will it really take to fill the bath?

It is possible to predict how a real system will behave. In this section I show how to calculate what will happen in the two-storey house design described earlier. Each step is explained in some detail in order to make it easier to adapt the calculation to the different problem you may be trying to solve.

Pipes often go round corners

The pressure driving the water along the pipes is the head. For the bath, this is 3 metres (say), and for the kitchen sink on the floor below it's 5 metres (say). This pressure is opposed by the friction losses in the pipes, which can be thought of as the pressure-difference-per-metre needed to push the water along at the flow rate you want. The log-log graph can be used to find the flow rate in a pipe run when the head is known.

There is one small difficulty. Real pipe goes round corners, and through tees, and valves, and other fittings. Each fitting creates its own bit of turbulence and absorbs some energy. How can this be taken into account?

Quite easily, as it happens. In just the same way that a length of straight pipe needs a pressure difference to push water through it, so does an elbow, or a valve. The pressure difference required across a 15mm elbow to move water though it at, say, 0.2 litres/sec can be measured. Whatever this number is, it must be the same as the pressure difference required to move water through some length of straight 15mm pipe at the same speed. In fact, this equivalent length is about 0.4 metres for a 15mm elbow. So the pressure drop in the elbow can be included by pretending that the 15mm pipe is really straight, but 0.4 metres longer than it actually is. The "equivalent lengths" of some common fittings are listed below.

Table 5: The equivalent lengths (in metres) of some standard fittings

Pipe size	Elbow	Tee: through	Tee: into branch	Tee: from branch
15 mm	0.4	0.05	0.7	0.6
22 mm	0.6	0.09	1.1	1.0
28 mm	0.9	0.12	1.6	1.4

One common fitting that doesn't appear in the table is the shower head. Its function is to take the stream of water flowing in a 15mm pipe and split it into many little streams, each about 1mm in diameter. This process takes a lot of energy. In terms of equivalent pipe length, a shower head might represent as much as 10-20 metres of 15mm, or even more, and this has a serious impact on flow-rate. That's why many people opt for a pumped shower, or one run directly from mains pressure via a combi boiler.

Example - the kitchen sink feed from the bathroom

The 15mm pipes run under the bathroom floor, then down to the ground floor, along to the sink, then up again to the taps.

There are 5 elbows (right-angle bends) in each pipe. According to Table 5, each elbow causes the same pressure drop as 0.4 metres of 15mm pipe. So the elbows represent 5 x 0.4m = 2m of pipe. The pipes themselves are about 7m long, so the total equivalent length of each one is 7m + 2m = 9m of pipe.

Then from the log-log graph, to achieve a water flow rate of 0.3 litres/second, the head would have to be 9m x 4,000 N/sq.m = 36,000 N/sq.m.

Pipes are different sizes, too

Suppose someone turns on the cold tap at the kitchen sink. What will happen?

Water will begin to flow out of the header tank, down the 28mm pipe to the cylinder, along the 22mm pipe to the bath, then down the 15mm pipe to the sink. How fast it flows depends on the head and the opposing frictional pressure drop. The head is known to be 5m, but the opposing frictional loss must be calculated.

The problem is that each different pipe size offers a different resistance to the same flow rate. What's needed is some way of expressing these different resistances in some common unit, so that they can be just added together.

A clue comes from the log-log graph. The lines are (nearly) parallel. This means that the rate of pressure drop (RPD) for 22mm pipe (say) is always some fraction of that for 15mm pipe, at the same flow rate.

At 0.05 litres/sec, 15mm pipe has a RPD of about 150 N/sq.m/m, whilst for 22mm RPD is just 20 N/sq.m/m - about seven times smaller.

(RPD for 15mm pipe) / (RPD for 22mm pipe)  =  7 / 1

And at 0.2 litres/sec the figures are 1900 and 270 - again, a ratio of about 7 to 1. So to get the same flow rate, 15mm pipe needs seven times the pressure difference that 22mm needs!

1m of 15mm pipe behaves like 7m of 22mm pipe.

These figures aren't exact, but they're near enough to be useful in the real world.

1m of 22mm pipe behaves like (1/7)m - 0.13m - of 15mm pipe.

The idea can be extended to the other pipe sizes. The table below shows the length of each standard size pipe that is equivalent to a 1 metre length of 15mm pipe. It says, for example, that just 3.5cm of 28mm pipe has the same pressure drop as 1m of 15mm pipe.

Table 6: The lengths (in metres) of standard pipe sizes equivalent to 1m of 15mm

10 mm	15 mm	22 mm	28 mm	35 mm	42 mm	54 mm
7	1.0	0.13	0.035	0.012	0.0047	0.0013

Flow rate calculations

So, back at the sink...

The question was, how fast will water come out of the cold tap at the kitchen sink?

The 15mm section runs from the kitchen tap itself up to the tee with the bath tap. It is about 7m long with five elbows, so it has an equivalent length of

[15mm actual]  =  7.0m (the pipe) + (5 x 0.4m) (the elbows)  =  9.0m.

The 22mm section includes two tees, and the pipe itself. If the 22mm pipe is (say) 3.5m long, this represents an equivalent length of

[22mm actual]  =  3.5m (the pipe) + (0.09m + 1.1m) (the tees: 1 in, 1 through)  =  4.7m.

[Convert 22mm actual --> 15mm equivalent]  =  4.7m x 0.13  =  0.6m.

The 28mm pipe is 6m long, with two elbows, giving an equivalent length of

[28mm actual]  =  6.0m (the pipe) + (2 x 0.9m) (the elbows)  =  7.8m.

[Convert 28mm actual --> 15mm equivalent]  =  7.8m x 0.035  =  0.3m.

So the total equivalent length of 15mm pipe is:

9.0m (15mm) + 0.6m (22mm) + 0.3m (28mm) = 9.9m.

Now, the head is 5m, and we know that:

Pressure  =  Length x Density x g

so putting in numbers for density and g, the pressure at the kitchen tap will be:

5 [m.of water] x 1,000 [kg/m³] x 9.8 [m/sec²]  =  49,000 N/sq.m

This pressure drop is shared out along the pipe run - that is, along the 9.9m equivalent length of 15mm - which means the average rate of pressure drop is

49,000 / 9.9 = 5,000 N/sq.m per metre

more or less. From the log-log graph, 15mm pipe with a RPD of 5,000 N/sq.m per metre has a flow rate of about 0.35 litres/second. This is what will come out of the tap, and more by luck than by skilful design, it's close to the 0.3 litres/second that it should be.

But is this figure true? Cross-check the result by working backwards. Breaking it down, the answer says that the 9m of real 15mm pipe accounts for (9 x 5,000) = 45,000 of the 49,000 N/sq.m of available pressure, the 22mm length takes (0.6 x 5,000) = 3,000 N/sq.m, and the 28mm needs (0.3 x 5,000) = 1,500 N/sq.m. This adds up to 49,500, which is close enough to the expected figure of 49,000. This is supposed to be engineering, not physics.

Then the flow rate in the actual 4.6m of 22mm pipe at its RPD of (3,000 / 4.6m) = 652 N/sq.m per metre is, from the log-log graph, about 0.35 litres/second. And for the actual 7.8m of 28mm at its RPD of (1,500 / 7.8) = 192 N/sq.m per metre, the flow is once again 0.35 litres/second. Each pipe is carrying the same flow rate, as it should do. So the kitchen sink tap really will deliver 0.35 litres/second.

What if the pipes are too noisy?

In a different design - perhaps one with with fatter pipes, or fewer elbows, or a larger head - the calculation might have predicted a much higher flow rate. In that case you would expect the pipes to be noisy when the water is running. To make them quieter, the water has to be slowed down, and this is actually very easy to do. Any competent plumber installing a system will have included valves at strategic points, so that sections of the system can be isolated - when, for example, you need to change a tap washer.

All you have to do is find the right valve and turn it down a bit. The extra resistance this adds will reduce the flow rate to a more sensible value. Halving the flow rate would reduce the noise by a factor of four.

Running a bath

This calculation is a bit more complicated, because it involves both the hot and cold water pipes in the two-storey house sketched above. The approach is exactly the same: find the equivalent lengths, convert them to the same size pipe, add them up, find the pressure drop per metre, look up the corresponding flow rate.

Cold feed only: Think about the cold water first. The 22mm pipe from the tap is 3.5m long and includes two tees. It has an apparent length of:

[22mm actual]  =  3.5m + (1.1m + 1.0m)  =  5.6m.

Similarly, the apparent length of the 28mm pipe is:

[28mm actual]  =  6.0m + (2 x 0.9m)  =  7.8m.

Since there is no 15mm pipe involved in the runs to the bath, it seems silly to convert these lengths to their equivalent 15mm lengths, then add them together, then convert them back again to 22mm. Instead, I'll simply convert the 28mm length to its equivalent 22mm value, using the figures in Table 6:

[28mm actual --> 22mm equivalent]  =  7.8m x (0.035 / 0.13)  =  2.1m.

Then the total equivalent length of 22mm is:

5.6m + 2.1m = 7.7m.

The head is 3m, which corresponds to a pressure of:

3 [m.of water] x 1,000 [kg/m³] x 9.8 [m/sec²]  =  29,400 N/sq.m

So the average rate of pressure drop is:

29,400 / 7.7 = 3,800 N/sq.m per metre

which according to the log-log graph means a (rather noisy) flow rate of close to 0.9 litres/second for a cold bath, rather than the 0.5 litres/second one might have hoped for. Still, things will change when the hot tap is running too.

Hot feed only: Now for the hot water. The hot pipe is all 22mm, which makes it slightly easier. The pipe run to the top of the cylinder is (let's say) 6m long, and includes two tees and three elbows. So:

[Hot: 22mm actual]  =  6m + (1.1m + 1.0m + [3 x 0.6m])  =  9.9m.

However, the hot water leaving the cylinder is replaced by cold water flowing from the header tank. The cylinder itself is only a kind of fitting, and it too has resistance, just like an elbow. The resistance of the whole circuit must be calculated.

The 22mm run is only 1m or so, plus a tee and an elbow. The cylinder's resistance is equivalent to about 1.6m of 22mm pipe. Adding these up gives:

[Cold: 22mm actual]  =  1m + (1.0m + 0.6m + 1.6m)  =  4.2m.

Finally, there's the 28mm pipe from the header tank. I've already calculated that this is 7.8m (actual) and 2.1m (22mm equivalent), so the total equivalent length of 22mm pipe in this circuit is:

9.9m + 4.2m + 2.1m = 16.2m.

The head is still 3m, or 29,400 N/sq.m, so the average rate of pressure drop is

29,400 / 16.2 = 1,800 N/sq.m per metre

which the log-log graph says represents close to 0.6 litres/second for a hot bath - pretty much what it should be. The flow rate from the hot tap is less than from the cold tap because of the resistance of all the extra pipe this water has to flow through.

Both hot and cold: Most people turn on both taps when they are running a bath. What happens then? It's a more difficult problem, because now the 28mm pipe from the header tank is carrying cold water both to the bath and to the bottom of the cylinder. A higher flow rate means a greater resistance. How much greater? That depends on the flow rate it's carrying, and that in turn depends on its resistance!

Breaking this circle demands a little algebra, since there are now two unknown (and inter-dependent) quantities: the flow rates from each of the bath taps. I don't know yet what they are, so I'll call the flow rate out of the hot tap H litres/sec, and that from the cold tap C litres/sec.

Now, the hot water circuit runs from the tee (with the 28mm pipe) up through the cylinder, down and along to the hot tap. It has an equivalent length of (9.9m + 4.2m) = 14.1m. This pipe run is carrying H litres/sec.

Similarly, the effective length of the cold water circuit, from the cold tap to the same junction, is 5.6m. This pipe run is carrying C litres/sec.

And the 28mm pipe, with an effective length of 7.8m (or 2.1m of 22mm equivalent), has to carry (H + C) litres/sec.

I know that H and C must be less than 0.6 and 0.9 litres/sec respectively, because those are the flow rates with only one tap open. The flow rates with both taps open must be smaller, because the hot and cold flows share space in the 28mm pipe, and it will offer greater resistance to the flow, so (for now) guess that H = 0.5 litres/sec. From the graph, this implies a Rate of Pressure Drop (RPD) of 1,400 N/sq.m per metre.

The effective length of the pipes carrying just hot water is 14.1m. The total pressure drop along these pipes would then be (14.1 x 1,400) = 19,700 N/sq.m. The head is 29,400 N/sq.m, so the pressure difference between the water surface in the header tank and the junction of the hot and cold circuits - at the tee near the bottom of the cylinder - would be (29,400 N/sq.m - 19,700 N/sq.m) = 9,700 N/sq.m. I'll come back to this figure in a moment.

But the same pressure of 19,700 N/sq.m that drives the hot water flow is driving the cold water flow too. The effective length of the pipes carrying just cold water is 5.6m, so the RPD for the cold-water pipes is (19,700 / 5.6) = 3,500 N/sq.m per metre, and the graph says that this implies a flow rate of about C = 0.82 litres/sec.

My original guess was that H was 0.5 litres/sec, and this guess resulted in a predicted value for C of 0.82 litres/sec. In other words, C is 1.64 times bigger than H. But this ratio depends only on the pipe layout. It's independent of the actual values of H and C. Whatever the real figures are, this ratio will stay the same.

If my original guess that H was 0.5 litres/sec had been correct, then the combined flow in the 28mm pipe would have been (0.5 + 0.82) = 1.32 litres/sec. The graph says that the RPD of 28mm pipe carrying 1.32 litres/sec is about 2,700 N/sq.m per metre, so the total pressure drop along its effective length of 7.8m is (2,700 x 7.8) = 21,000 N/sq.m.

But I have already calculated that if H really had been 0.5 litres/sec, the pressure drop along the 28mm pipe would have been 9,700 N/sq.m - only half as much. The original guess was plainly wrong! So how can the problem be solved?

A Useful Approximation

The relationship between the two quantities of interest - flow rate and pressure drop - is extremely complex, but fortunately it can be approximated by a rather simple formula:

Rate of Pressure Drop (RPD)  =  A x (Flow Rate)² + B

- where A and B are constants that depend only on pipe size. I give values for A and B in the table below.

Table 7: Values of constants A and B in the Useful Approximation

Pipe size	10mm	15mm	22mm	28mm	35mm	42mm	54mm
A	400,000	44,000	5,300	1,400	450	160	40
B	100	70	40	30	18	20	14

The approximation is accurate when the pipe is carrying a flow rate of between 30% and 100% of its maximum capacity.

Running the bath

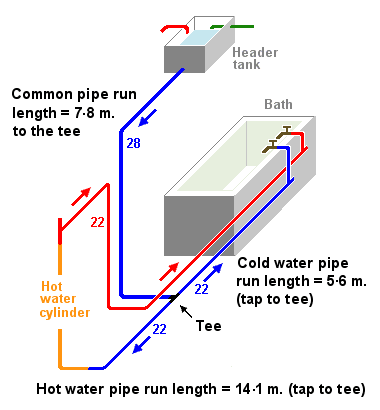
Here is a simplified diagram showing only the pipe runs to the hot and cold bathtaps. Water is flowing from both taps.

The cold water feed pipe is 5.6 metres long and carrying C litres/second. The hot water pipe is 14.1 metres long and carries H litres/sec. The common feed, carrying cold water to the tap and also into the bottom of the cylinder - that is, (C + H) litres/sec - is 7.8 metres long, from the header tank to the tee.

Now, from the Useful Approximation, the total pressure difference between the ends of a pipe is

Pressure drop in pipe = Length x [A x (Flow Rate)² + B]

The hot and cold pipes are both fed from the common pipe, and both end in open taps. The pressure difference between the common point and each tap must be the same. So by applying the formula, doing a bit of algebra, and discarding terms that are too small to matter, we get a relationship between the flow rates that just depends on pipe lengths:

This is really just a more formal way of expressing the idea that the hot and cold flow rates will always bear the same ratio to each other. But we also know that, for the whole system:

Head = (Pressure drop in common pipe) + (Pressure drop in hot [or cold] pipe)

and this, with a bit of algebra, can be made to yield an expression for the actual hot or cold flow rate in terms of numbers we already know! To make the equation as general as possible, I have used the symbols L_c and L_h to stand for the lengths of the cold and hot pipe runs respectively, and L₂₈ to mean the length of the common 28mm pipe. For the cold flow rate, C, the equation is:

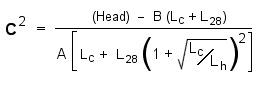
This equation looks forbiddingly complex, but finding a value for C is simply a matter of substituting known numbers for all the variables and calculating the answer. The head is 29,400 N/sq.m., L_c is 5.6m., and L_h is 14.1m. It's important that all the lengths be expressed in the same units, so L₂₈ is 2.1m (of 22mm equivalent) rather than the actual figure of 7.8m. Finally, from Table 7, the constants for 22mm pipe are A = 5,300 and B = 40.

The answer I got was C² = 0.49 litres/second, so C = 0.7 litres/second. And since (C / H)² = (14.1 / 5.6), I calculate that H = 0.44 litres/second.

The answer can be checked by working out the individual pressure drops using the Useful Approximation. In the hot and cold pipes:

Cold pipe: Pressure drop = 5.6m x [5,300 x (0.7)² + 40] = 14,800 N/sq.m

Hot pipe: Pressure drop = 14.1m x [5,300 x (0.44)² + 40] = 15,000 N/sq.m

which is near enough the same, as it should be, and in the common pipe,

Common pipe: Pressure drop = 2.1m x [5,300 x (0.7 + 0.44)² + 40] = 14,500 N/sq.m

making a total of about 29,500 N/sq.m. The actual head is 29,400 N/sq.m. I think the conclusion is that the sums really do add up. The method works.

If you want another look at the theoretical background to all this, you'll find it here in Part 1.