What's a capacitor?

A capacitor is a component designed to create and hold an electric field, which means that capacitors can store energy . It takes energy to pull electric charges apart and so establish an electric field between the separated charges. With the charges held apart, the energy is stored in the electic field, and when the charges are allowed to move again, the stored energy becomes available to do something useful. Capacitors are like little batteries.
What's an electric field?
The region of space around isolated electric charges appears distorted, and makes objects in it behave in unexpected ways. Engineers and physicists use the phrase electric field when they want to talk about this effect.
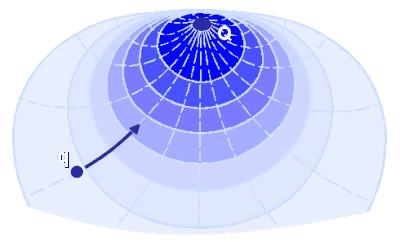
This sketch is trying to illustrate that pushing the little charge q nearer to Q takes more and more effort as the charges get closer together.
I've written here about the idea of charge - what it was thought to be, how Coulomb established that charge exerts force, and how Millikan proved that all electrons carry exactly the same amount of charge.
It's not straightforward to describe what an electric field actually is. It's easier to say what it's like. There's an analogy with gravitation. The force between two charges (here, Q and q) obeys an inverse square law, as does the force between two masses. Einstein saw gravitation as the result of space being distorted due to the presence of mass, and it's an obvious step to see the presence of charge as having a similar distorting effect.
Professor Carter offers this thought:
We may say, if we will, that the charges are physically real things, endowed with the power of acting on one another at a distance; the electric field on the other hand is not a physical reality but a philosophical idea, convenient in calculation. Alternatively we may say that the electric field is the chief physical reality, and that a charge is entitled to be called real only because it is associated with a field through which it may be recognised and measured; on this view, the observed force between charges is ascribed to the interactions of their fields. The "action-at-a-distance" theory was the standpoint of Coulomb and Ampere; the "field theory", of Faraday and Maxwell.
Professor Harnwell uses fewer words:
An electric field is said to be present in a region if a small test charge placed there experiences a mechanical force.
And Professor Kraus is even more succinct:
An electric field is a region where forces act.
If it's not too poetic and fanciful an idea, you might even think of the electric field as the longing felt by separated charges that yearn to be together again. But whether the electric field is 'real' or not, it's a convenient way of imagining the stresses in a region of space, just as the idea of gravitation helps in predicting how objects will behave.
How strong is the field?
The force exerted by a field (and the force is how we know that there is a field) depends mainly on the amount of charge that's causing it.
Coulomb showed that the force depends on the sizes of the charges (in the drawing above, the charges are Q, causing the force, and q, experiencing it), and r, the distance between them. K is just a constant, selected to make the answer come out right with the chosen units - usually Newtons, Coulombs & meters.
But the idea that an object can move another object without touching it - "action at a distance" - defies common sense. To explain it, physicists came up with the analogy of water flow. Suppose the single isolated charge in the sketch above was actually squirting out some invisible magic fluid in all directions. (They called this fluid "electric flux".) If the flux happens to push against another charge, that charge would move. Flux has to be caused by the charge creating the field (Q in the drawing) so it's possible to calculate how much flux a given charge will generate, and so calculate the force on the little charge q.
Unfortunately, the universe is a bit more complicated than that. It turned out that the force on q also depended on the environment in which the force was acting. The force in air is slightly different to that in a vacuum, for example. To make the sums add up, physicists invented a fiddle factor, called it "permittivity" and labelled it ε.
Suppose q is so tiny that its presence does not disturb the field to any noticeable extent. The force on q is then dominated by the field created by Q. The big charge Q exerts a force on q (because q is a charge too), but Q establishes a potential force at that point whether q is present or not. The field around Q exists even when q isn't there.
So it's possible to imagine the concept of field strength - the field intensity at a point in the field - by thinking about the potential force that would be applied to q if it happened to be present:
The little hypothetical test charge q has now disappeared from the equation, as it should have done. The field strength E at a distance r from Q depends on Q (and ε, of course - here I use ε0 as a shorthand way of saying "as long as you measure the force in a vacuum"). The term in brackets is just the constant I've been calling K.
Are flux and field the same thing?
Not quite. Flux is the imaginary fluid pouring out of a charge, whilst the field represents the force on a test charge in the path of the flux.
The new constant ε0 is called the "permittivity of a vacuum", and it's there as a reminder that the electric field intensity depends on the material in which the electric field is acting. Different materials have different permittivities, just as they have different densities.
In fact, permittivity is the link between flux and field strength. Flux density (D) is field strength (E) x permittivity. In other words, the strength of the field caused by Q is reduced - the force on a test charge q is smaller - when the field acts through something other than a vacuum. Wax, for instance, has a permittivity of about 2.
If q was buried in the middle of a block of wax near Q, it would move more sluggishly than if it were in air, and that sort of makes sense.
It's important to remember too that q tries to move directly away from (or towards) Q because positive charges repel each other. So the field intensity E has direction as well as magnitude. So does D.
What's a volt?
Suppose that both q and Q are positive charges, and I try to push them closer together. They resist this, so it takes effort. I have to apply energy - do work - to make it happen. (For some reason, physicists and maths teachers prefer to think in terms of "doing work", whilst engineers prefer the idea of "energy". We're all talking about the same thing. Energy is measured in joules, and so is work.)
Suppose I manage to push the little charge q a tiny distance δr towards Q. According to the maths teachers,
and this amount of work (measured in joules) is the amount of potential energy (also measured in joules) that I have given to the little test charge q by moving it "uphill" towards Q across the short distance δr.
But the field is there whether I move the charge or not, and its strength E varies with the distance from Q. So there must be a difference in potential energy (or just 'potential') between any two points in the field. Moving a charge between them involves supplying (or maybe receiving) energy.
It would be possible at this stage to calculate the absolute potential at a point - the energy it would take to move a charge from infinity to the point - but that seems, well, pointless. A builder doesn't need to know the distance from the centre of the earth in order to put up a house with level floors. Potential difference is what matters. Potential difference implies a difference in energy levels between the two points. Connect a load between them and energy will flow.

Potential is an enormously useful concept. It is measured in volts (which as the equation suggests is the same thing as joules per coulomb). So the electric field intensity E could be expressed in Newtons per Coulomb, but it's often much more convenient to think of it in terms of Volts per meter - that is, the voltage difference between two points one meter apart.
Volts, at last!
Almost everyone must have seen a voltmeter. It exists to measure the potential difference between two points. Strictly, it measures the amount of energy that would be needed to move a charge of 1 Coulomb between the two points, but that's rather a complicated and hypothetical idea. Many engineers find it simpler to see the voltage itself as the reality - it's easier to think in terms of something you can measure.
What's capacitance?
Capacitance is a measure of how much charge is needed to produce a given potential difference between two separated conductors. When each conductor has 1 Coulomb (C) of charge, and this leads to a potential difference of 1 volt existing between them, the pair of conductors is said to have a capacitance of 1 Farad (F).
If a charge of just 1 μC is sufficient to produce this potential difference, the capacitance is 1 μF. In other words, capacitance is defined as the ratio of the amount of charge stored to the resulting voltage difference.
What do capacitors look like?

Capacitors can be bought in a range of values from 1 pF (one million-millionth of a Farad) to several thousand microfarads (oddly, engineers don't use the term "millifarads"). Some special capacitors, intended to be used instead of batteries, are available in values up to 1 F. Manufacturers also specify the maximum allowed working voltage for their components. Applying too high a voltage will cause catastrophic failure in a capacitor.
What does capacitance depend on?
Since 'capacitance' is just another way of talking about the electric field that exists between conductors, you would expect its value to depend on the distance between the conductors and their area of overlap, and it does.
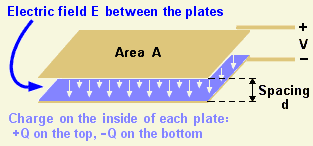
The simplest capacitor has two parallel plates, separated by an insulator, like this. The separated charges (+Q & -Q) cause an electric field E to appear between the plates, which shows up on the voltmeter as a voltage difference V.
The charge Q (measured in Coulombs) is spread evenly across each plate, like butter on a slice of bread, so we can think of the charge density - how tightly the charges are squashed together - in Coulombs per square meter. Call this ρ, so that the total charge Q is ρA Coulombs.
The even distribution of charge means that the electric field E will be the same at all points between the plates, and so the potential difference between the plates is Ed volts. The field between the plates is uniform, so the flux density D will be the same as the charge density ρ on the plates.
![]() So, given the definition of capacitance as C = Q/V, we can subsitute for Q and V to get a nice, simple answer.
So, given the definition of capacitance as C = Q/V, we can subsitute for Q and V to get a nice, simple answer.
The insulating material between the plates is known as the dielectric, and the symbol ε is used for its permittivity (or 'dielectric constant'). Many substances have ε > 1, so by choosing the right dielectric, manufacturers can pack more capacitance into a smaller volume. Typical dielectrics include ceramics (for when space matters) and plastics (for when precision is more important).
How do you make a capacitor?
 Most capacitors consist of two parallel plates separated by an insulator. Sometimes the resulting sandwich is rolled up into a tube, like a Swiss roll, to save space, and some capacitors have multiple layers, like a club sandwich. The variable capacitor shown on the right has a moveable vane that can be rotated between fixed vanes so that the amount of overlap - the effective area - can be varied as required.
Most capacitors consist of two parallel plates separated by an insulator. Sometimes the resulting sandwich is rolled up into a tube, like a Swiss roll, to save space, and some capacitors have multiple layers, like a club sandwich. The variable capacitor shown on the right has a moveable vane that can be rotated between fixed vanes so that the amount of overlap - the effective area - can be varied as required.
Sometimes capacitance appears all by itself in a circuit. A designer must be careful of the stray capacitance between wires, between tracks on a board, and even between adjacent components. All the metal components of a circuit have stray capacitance between them, and energy will leak across though it. A working circuit is a frothing sea of electric fields.
Sources
The electromagnetic field in its engineering aspects - G.W. Carter (Longmans, 1954)
Principles of electricity and electromagnetism - Gaylord P. Harnwell (McGraw Hill, 1938)
Electromagnetics - John D. Kraus (McGraw Hill, 1991).
