
This article shows how to calculate the time constant of a CR network, and why it's useful to know it.
How long does it take to charge a capacitor?
A capacitor is a container for electric charge, so the answer depends on how big the container is, and how fast you allow charge to flow into it. How long does it take to fill a bucket?
Why should you limit the charging rate?
If you don't, you could damage either the capacitor or the power source. Big electrolytic capacitors intended for use in switched-mode power supplies have an internal resistance measured in milli-ohms. If this is the only resistance in the circuit, there could be a huge current spike as the capacitor begins to charge.
How fast does a capacitor charge?

Here's a capacitor C being charged from a power supply, with all the instantaneous voltages labelled so that I can set up the equations and explore what's happening.
When power is first applied, the capacitor holds no charge, so there's zero voltage across it (vC = 0). This means that all the applied voltage appears across R, so the current at switch-on is V/R. If V is 10v and R is 50 mΩ (that is, if the only resistance in the circuit is the capacitor's internal resistance) the initial current spike would be 20 amps! Are you sure the capacitor could handle this?
Setting up the equation
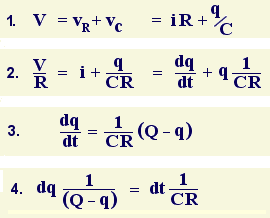
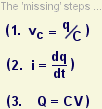
1. The first step is to add up the voltages and write an equation that links them together, then express vR and vC in terms of current and charge.
2. Next, divide through by R, and rewrite current as rate-of-change of charge.
3. The maximum possible charge the capacitor could hold in this circuit is C V, so it makes sense to write this as Q and simplify the equation a little.
4. And finally, separate the variables. The equation is ready to be solved. I'll have to use integration, because each of the little dq's is different. As the capacitor charges, it gains voltage, so as time passes the charging current gets smaller and smaller. (In fact, current never really stops flowing - it just shrinks past the point of being measurable.)
Solving the equation
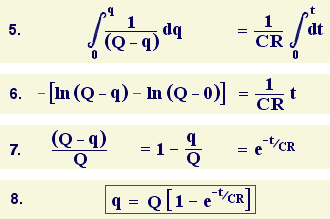
5. So, put in the integral signs, and the limits. I want to discover the amount of charge q at any time t as the capacitor charges.
6. Doing the integration and putting in the limits shows that the relationship between q and t is logarithmic (ln means natural logarithm - that is, log to the base e.)
7. Raising each side to the power e simplifies things ...
8. ... and I end up with q, expressed in terms of its maximum possible value (Q) and describing how it varies with time t during charging.
What does the answer mean?
Faced with an equation like this, my first instinct is to check what happens at the limits. What is q when t is zero? What happens when t is infinite? In other words, does the answer seem sensible?
When t is zero, the term e-t/RC becomes e0, which is 1, and 1-1=0, so the right-hand side of the expression simplifies to 0. So q is zero - the capacitor holds no charge - before I switch on the power. Then when t is infinite, the term e-t/RC becomes e-∞, which is 0, and 1-0=1, so the right-hand side of the expression simplifies to Q. So q would become Q - the capacitor would become fully charged - if I waited long enough. So the equation says that q rises from 0 to its final value of Q, which is of course what I specified in the integral.
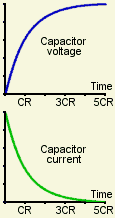
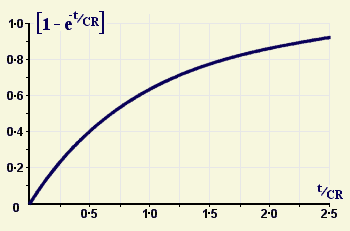 Here's an exponential curve like the one in the equation. I've simplified things slightly by assuming that Q is 1, and using as the horizontal scale the ratio of t to CR.
Here's an exponential curve like the one in the equation. I've simplified things slightly by assuming that Q is 1, and using as the horizontal scale the ratio of t to CR.
This ratio must be a number. Since t is time, CR must be a time, too. What matters is not t alone, but the value of t as a fraction of CR. And the value of CR depends solely on the values of capacitor and resistor in this particular circuit. CR is known as the circuit's time constant. For example, if C is 10 μF and R is 1 MΩ, the time constant is 10 seconds. Microfarads times megohms equals seconds.
After a time equal to CR - one time constant - the capacitor has charged to 63%. That's not particularly interesting or useful. It might have been better to define, say, 3CR as the time constant, because after 3CR the charge has reached 95% of its final value.
But CR is easy to remember, and it's the reciprocal of the network's corner frequency which is a useful idea when you're thinking about how RC networks affect a circuit's frequency response. I discuss this further in the articles on RC network theory.
And since the voltage across the capacitor is proportional to the charge it's holding, this exponential curve also shows how the capacitor voltage varies with time.
Single-pulse generator
And here's an example to show how time constant is used in practice ...
The need often arises to generate a single fixed-length pulse in response to a trigger event. For example, many audio amplifiers do not connect the loudspeakers until the power rails have stabilised, to avoid a disturbing 'thump' from the speakers.
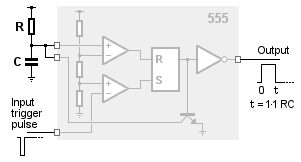 One way of generating a single pulse is to use a 555 timer chip.
One way of generating a single pulse is to use a 555 timer chip.
Whilst the circuit is waiting for a trigger pulse, the RS flipflop is held reset. Its output is high, so the transistor conducts, placing a short-circuit across the capacitor C and so preventing it from charging. The output of the 555 itself is low at this time, due to the inverting buffer.
As soon as the trigger pulse arrives, the lower comparator sets the RS flipflop. The output changes state, switching off the transistor, and the capacitor begins to charge through R. Eventually the voltage across C reaches a preset threshold value. The upper comparator then resets the flipflop, ready for the next trigger pulse.
